![[Stable]](figures/lifecycle-stable.svg)
First, it will determine whether the data is uni-dimensional or multi-dimensional using parameters::n_factors(). If the data is uni-dimensional, then it will print a summary
consists of alpha, G6, single-factor CFA, and descriptive statistics result. If it is multi-dimensional, it will print a summary consist of alpha, G6, omega result. You can
bypass this by specifying the dimensionality argument.
reliability_summary(
data,
cols,
dimensionality = NULL,
digits = 3,
descriptive_table = TRUE,
quite = FALSE,
streamline = FALSE,
return_result = FALSE
)Arguments
- data
data.frame- cols
items for reliability analysis. Support
dplyr::select()syntax.- dimensionality
Specify the dimensionality. Either
uni(uni-dimensionality) ormulti(multi-dimensionality). Default isNULLthat determines the dimensionality using EFA.- digits
number of digits to round to
- descriptive_table
Get descriptive statistics. Default is
TRUE- quite
suppress printing output
- streamline
print streamlined output
- return_result
If it is set to
TRUE(default isFALSE), it will returnpsych::alphafor uni-dimensional scale, andpsych::omegafor multidimensional scale.
Value
a psych::alpha object for unidimensional scale, and a psych::omega object for multidimensional scale.
Examples
fit <- reliability_summary(data = lavaan::HolzingerSwineford1939, cols = x1:x3)
#> Model Summary
#> Model Type = Reliability Analysis
#> Dimensionality = uni-dimensionality
#>
#> Composite Reliability Measures
#> ────────────────────────────
#> Alpha Alpha.Std G6 (smc)
#> ────────────────────────────
#> 0.626 0.627 0.535
#> ────────────────────────────
#>
#> Item Reliability (item dropped)
#> ─────────────────────────────────
#> Var Alpha Alpha.Std G6 (smc)
#> ─────────────────────────────────
#> x1 0.507 0.507 0.340
#> x2 0.612 0.612 0.441
#> x3 0.458 0.458 0.297
#> ─────────────────────────────────
#>
#> CFA Model:
#> Fit measure is not printed due to factor <= 3
#> Factor Loadings
#> ───────────────────────────────────────────────────────────────────────────────
#> Latent.Factor Observed.Var Std.Est SE Z P 95% CI
#> ───────────────────────────────────────────────────────────────────────────────
#> DV1 x1 0.621 0.067 9.223 0.000 *** [0.489, 0.753]
#> x2 0.479 0.063 7.645 0.000 *** [0.356, 0.602]
#> x3 0.710 0.071 9.936 0.000 *** [0.570, 0.850]
#> ───────────────────────────────────────────────────────────────────────────────
#> *** p < 0.001, ** p < 0.01, * p < 0.05, + p < 0.1
#>
#> Descriptive Statistics Table:
#> Model Summary
#> Model Type = Correlation
#> Model Method = pearson
#> Adjustment Method = none
#>
#> ───────────────────────────
#> Var x1 x2
#> ───────────────────────────
#> x1
#> x2 0.297 ***
#> x3 0.441 *** 0.340 ***
#> ───────────────────────────
#> Note: * p < 0.05, ** p < 0.01, *** p < 0.001
#>
#> ─────────────────────────────────────────
#> Var mean sd x1 x2
#> ─────────────────────────────────────────
#> x1 4.936 1.167
#> x2 6.088 1.177 0.297 ***
#> x3 2.250 1.131 0.441 *** 0.340 ***
#> ─────────────────────────────────────────
#>
fit <- reliability_summary(data = lavaan::HolzingerSwineford1939, cols = x1:x9)
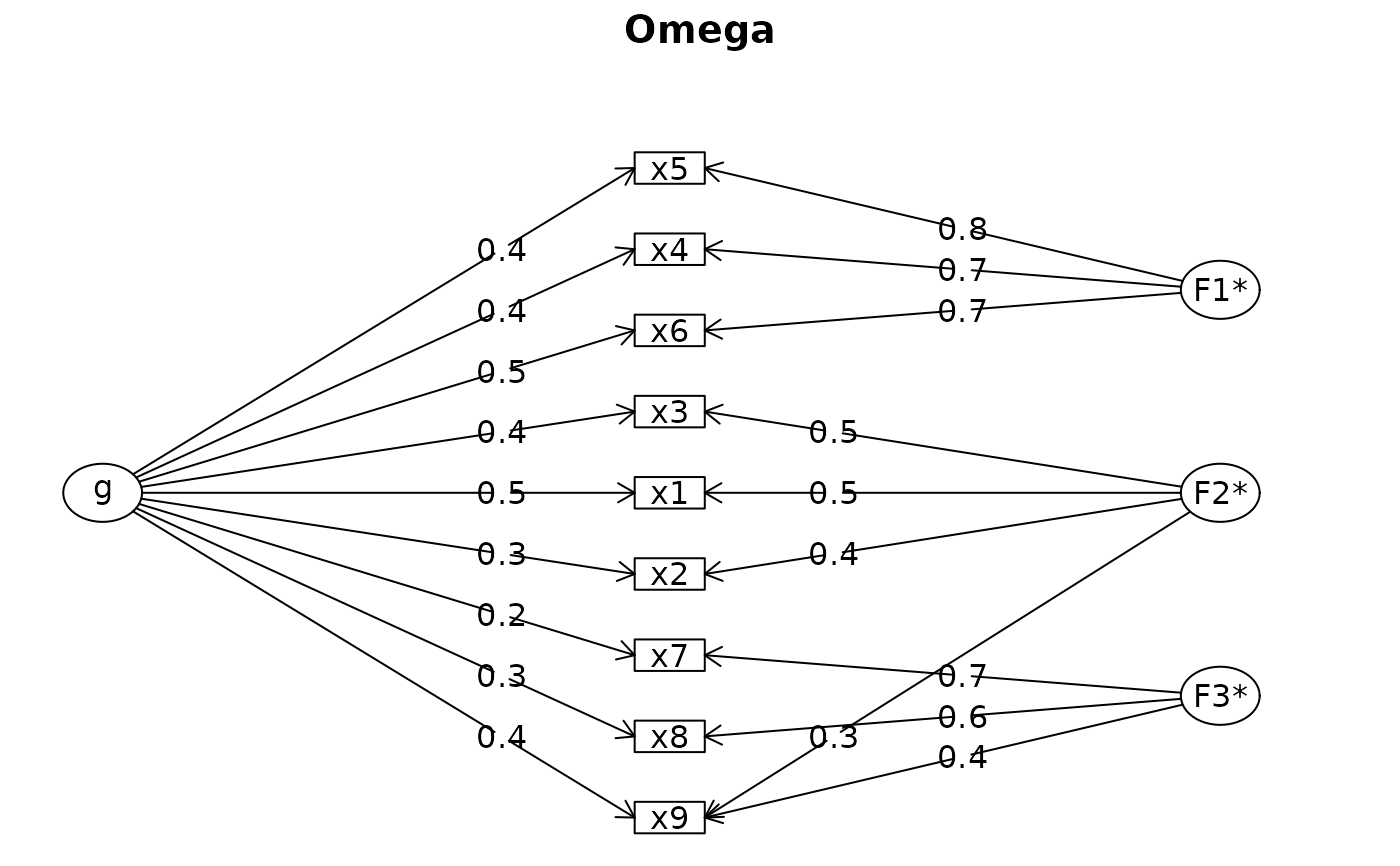#> Model Summary
#> Model Type = Reliability Analysis
#> Dimensionality = multi-dimensionality
#>
#> Composite Reliability Measures
#> ──────────────────────────────────────────────────────────
#> Alpha Alpha.Std G.6 Omega.Hierarchical Omega.Total
#> ──────────────────────────────────────────────────────────
#> 0.76 0.76 0.808 0.449 0.851
#> ──────────────────────────────────────────────────────────
#>
#> Item Reliability (item dropped)
#> ─────────────────────────────────
#> Var Alpha Alpha.Std G6 (smc)
#> ─────────────────────────────────
#> x1 0.725 0.725 0.780
#> x2 0.764 0.763 0.811
#> x3 0.749 0.748 0.796
#> x4 0.715 0.719 0.761
#> x5 0.724 0.726 0.764
#> x6 0.714 0.717 0.764
#> x7 0.766 0.765 0.800
#> x8 0.748 0.747 0.789
#> x9 0.731 0.728 0.782
#> ─────────────────────────────────
#>
#> Descriptive Statistics Table:
#> Model Summary
#> Model Type = Correlation
#> Model Method = pearson
#> Adjustment Method = none
#>
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────
#> Var x1 x2 x3 x4 x5 x6 x7 x8
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────
#> x1
#> x2 0.297 ***
#> x3 0.441 *** 0.340 ***
#> x4 0.373 *** 0.153 ** 0.159 **
#> x5 0.293 *** 0.139 * 0.077 0.733 ***
#> x6 0.357 *** 0.193 *** 0.198 *** 0.704 *** 0.720 ***
#> x7 0.067 -0.076 0.072 0.174 ** 0.102 0.121 *
#> x8 0.224 *** 0.092 0.186 ** 0.107 0.139 * 0.150 ** 0.487 ***
#> x9 0.390 *** 0.206 *** 0.329 *** 0.208 *** 0.227 *** 0.214 *** 0.341 *** 0.449 ***
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────
#> You can drag and resize the R console to view the entire table
#> Note: * p < 0.05, ** p < 0.01, *** p < 0.001
#>
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Var mean sd x1 x2 x3 x4 x5 x6 x7 x8
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> x1 4.936 1.167
#> x2 6.088 1.177 0.297 ***
#> x3 2.250 1.131 0.441 *** 0.340 ***
#> x4 3.061 1.164 0.373 *** 0.153 ** 0.159 **
#> x5 4.341 1.290 0.293 *** 0.139 * 0.077 0.733 ***
#> x6 2.186 1.096 0.357 *** 0.193 *** 0.198 *** 0.704 *** 0.720 ***
#> x7 4.186 1.090 0.067 -0.076 0.072 0.174 ** 0.102 0.121 *
#> x8 5.527 1.013 0.224 *** 0.092 0.186 ** 0.107 0.139 * 0.150 ** 0.487 ***
#> x9 5.374 1.009 0.390 *** 0.206 *** 0.329 *** 0.208 *** 0.227 *** 0.214 *** 0.341 *** 0.449 ***
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> You can drag and resize the R console to view the entire table
#>